1 INTRODUCTION

It is well known that the amount of induced radioactivity that will be produced in the LHC experiments will be much larger than in most previous high-energy physics experiments. It is also well known that most of the radioactivity produced will be close to the accelerator beamline. The aim of this note is to describe some of the estimations of the induced radioactivity in the region around the beampipe in ATLAS. Several small groups in ATLAS have worked on calculations of induced radioactivity but most of the results that will be presented here have been calculated by a group of physicist at the Moscow Engineering Physics Institute that have been contracted by ATLAS for this purpose. A web page [1] has been set-up with detailed information about all the ATLAS activation calculations and in this note only a small selections of the results will be presented. The conclusions in this note are those of the author and do not necessarily represent the opinions of the ATLAS collaboration. All results should be considered to be preliminary since the study is on going.

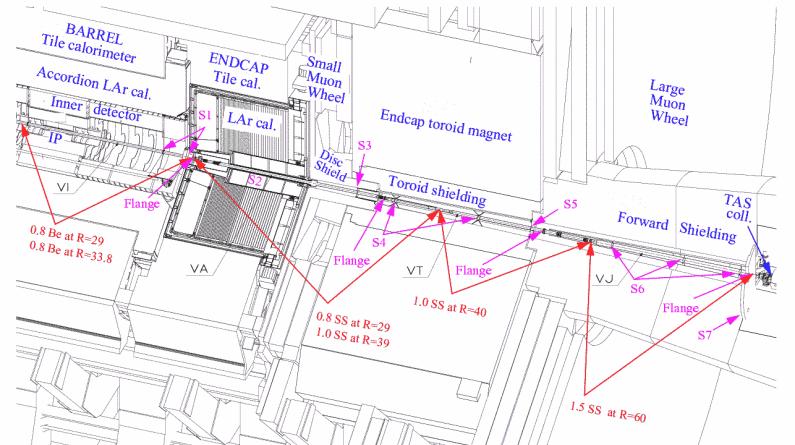
Figure 1: The drawing shows the detectors and shielding around the beam pipe in one half of the ATLAS experiment. The thickness and radius in mm of the beampipe is indicated as well as the beampipe material. When two values are given for a beampipe section this indicates that the beampipe has two walls. S1-S7 indicate the position of beampipe supports.

2 ACCESS SCENARIOS

It has been known for some time where in ATLAS the largest amount of induced radioactivity will be produced. It is, however, not necessarily the most radioactive areas that are the most troublesome for the experiment since these are not areas were maintenance work has to be carried out. It is the combination of radiation levels with the expected maintenance times which decides if an area is a potential problem for the experiment or not. As a general rule the radiation levels are the highest close to the beampipe and so the first thing to determine is what work will be needed to do around the beampipe. To understand this one has to understand the principle of the ATLAS access scenarios.

The ATLAS experiment has two main scenarios called the short and long access scenario. In the long scenario the beampipe is removed which is not the case in the short scenario. Figure 1 shows the detectors and shielding surrounding the beampipe in one half of the ATLAS experiment (between the interaction point (IP) and the TAS collimator). In both the long and the short access the massive forward shielding is first brought to the surface and stored and the large muon wheel is moved forward to the position of the TAS collimator. In case of the short access the beampipe support S5 has then to be removed and S4 has to be undone. The endcap toroid shielding can be moved into the place previously occupied by the forward shielding. The support S3 that is situated 0.5 m inside a narrow copper tube then has to be removed so that the small wheel followed by the endcap calorimeter can be moved forward. After these operations access can in principle be granted to the inner detector, the small muon wheel and the endcap calorimeter.

In case of the long access scenario the entire beampipe is removed with the exception of the beampipe inside the inner detector (VI). The removal start with the VJ beampipe that has a remotely operated flange on the TAS side but a normal flange that has to be removed manually on the toroid side. After the VJ is removed the S4 support is undone and the S5 support is replaced by a support that can slide against the toroid shielding surface. The endcap is moved back and the flange between the VA and VT beampipe sections is undone and the VT is removed. The S3 support is removed and the small muon wheel and the endcap calorimeter are moved forwards so that access is given to the flange between the VI and VA sections. The VA beampipe is then removed.

From the above description it is clear that the vacuum group has to work for a considerable amount of time in very close contact to the beampipe. It is also obvious that the short access scenario will result in much shorter exposure to radiation of the vacuum technicians than the long scenario in which the beampipe is removed. When it comes to the maintenance of the ATLAS experiment it is mostly work at the inner detector that will require technical personnel to spend time close to the beamline. The study of the radiation in ATLAS has therefore been aimed mostly at estimating the radiation levels in the areas where the vacuum and inner detector technicians have to work.

3 METHODS AND ASSUMPTIONS

Two methods were used to calculate the induced radiation in ATLAS. The first method uses the well-known relationship between the density of inelastic interactions (the so-called star density) and the dose-rate [2,3]. This approximative method, which is depicted in Figure 2, was used in an initial stage of the study to determine which of the massive shielding and detector elements were potential problem regions. The star-density was calculated [4] using the GCALOR code [5] under the assumptions of 7x7 TeV collisions and a luminosity of 10³⁴ cm²/s giving a p-p interaction rate of 8 x 10⁸ s^-1 as predicted by the PHOJET program [6]. Inelastic hadronic interactions with an energy above 50 MeV were counted as stars.

The second method [7,8] that was used by the MEPhI group was using the standard activation formula given in Figure 2. Particle flux maps were again produced [4] by the PHOJET and GCALOR programs [5] and used as inputs in the calculations. The calculations were made separately for (n,g) capture of low-energy thermal neutrons and high energy hadrons. In the latter case the lack of knowledge of the cross sections above 20 MeV for all possible types of interactions made it necessary to make the assumption that the cross section of all incident hadrons would be the same as that of protons [9]. The codes DOT-III [10] and MCNP [11] were used to calculate self-absorption and photon transport. Only gamma radiation was calculated. An LHC year was assumed to consist of 120 days of continuing running with a 245-day stop.

Figure 2: A summary of the two methods used to estimate the amount of induced radioactivity in the ATLAS experiment.

4 CONSIDERATIONS ABOUT THE CHOICE OF MATERIAL

The low-energy neutron activation is very much dependent on the material. The amount of radiation from silver can for example be 10000 times larger than that of the radiation from the same amount of lead due to differences in cross sections and half-lifes of the produced isotopes. As stated earlier it is, however, radiation from high energy hadron activation that dominates close to the beamline (<1-2 m) in ATLAS. Figure 3 shows how the activation by high energy hadrons is expected to vary with the atomic number for very long irradiation times i.e. when saturation is reached. Except for very light materials such as beryllium and carbon most materials give similar amounts of radiation. It can be noted that 1g of aluminium is predicted to give the same dose-rate as iron and only a factor 2 less than 1g of lead.

It can also be noted that the predicted values by Morev et al. are in a reasonable agreement with the ones calculated by Barbier back in 1969 [12].

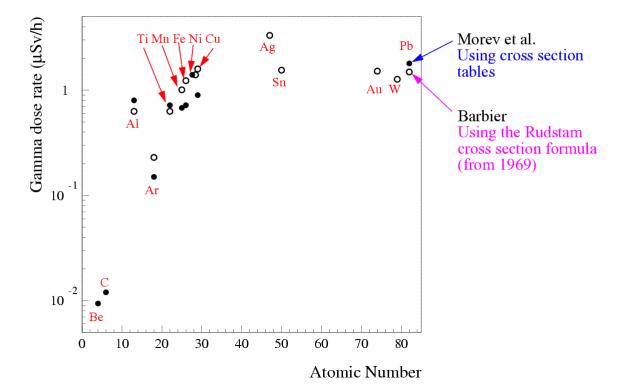
Figure 3:The calculated dose-rate from a point source of 1 g at a distance of 1 cm. The radioactivity was induced by 2.9 GeV protons (flux=10⁶ p/cm²). The dose-rate is after 5000 days of irradiation and 30 days of cooling-off.

To conclude from Figure 3 that the choice of material is completely irrelevant is not correct. Table 1 gives the ratio of the predicted dose-rate from the VA beampipe in ATLAS when it is made of stainless steel or aluminium. For long irradiation times the difference is small as noted previously but the shorter the irradiation time the larger the difference between aluminium and stainless steel. The reason for this is the different half-lifes of the most important activation products in steel (⁴⁸V t=16 days, ⁵²Mn t=5.6 days, ⁵⁴Mn t=312 days, ⁴⁶Sc t=84 days and ⁵⁶Co t=77 days) and aluminium (²²Na t =2.61 years and ²⁴Na t =15 hours). Due to the long half-life of ²²Na, aluminium reaches saturation much later than steel.

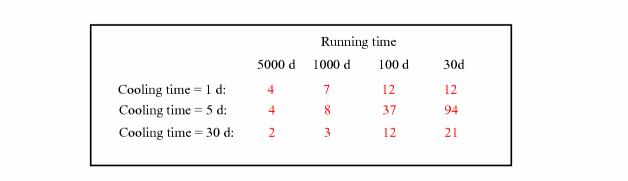
Table 1: The ratio of the expected dose-rate from a VA beam pipe in ATLAS made out of stainless steel compared to a beam pipe made out of aluminium.

5 RESULTS OF THE CALCULATIONS

Most of the areas where people have to work during access to ATLAS have now been studied. Only the region in front of the inner detector will be discussed here since it is one of the most problematic. The discussion will be limited to the radiation from the beampipe since this is the dominant source but radiation maps from the inner detector and the calorimeters are also available. For more information about this the reader is referred to the web page [1] mentioned in the introduction.

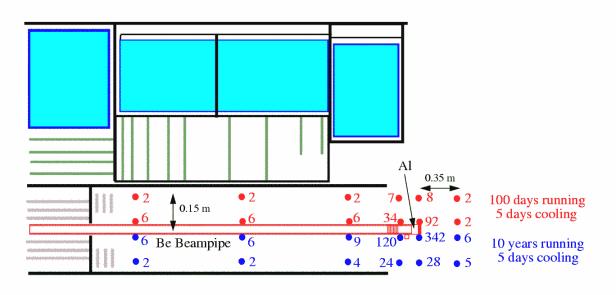
Figure 4: The expected dose-rate in mSv/h from the VI beam pipe that is situated inside the inner detector. The blue regions depict the TRT part of the inner detector, the green lines the SCT detector and the gray lines the pixel detector. The beam pipe is indicated in red.

Figure 4 show the result of a calculation of the radiation coming from the beampipe inside the inner detector. Most of the beampipe will be made from beryllium and the expected radiation from this part is negligible. At the very end of the beampipe there is a small section made from aluminium and here the expected dose-rate reaches values of 300 mSv/h after 10 years of running and at a distance of 1 cm from the beampipe.

The VA section of the beampipe that connects to the VI section is supposed to be made of stainless steel. As can be seen in Figure 5 the predicted rates are dramatically different from the dose-rate predicted for the VI section. At a distance of 1 cm from the beampipe the dose-rates varies between 3 and 11 mSv/h. As mentioned earlier only gamma radiation has been calculated and since the beampipes are made of thin materials one can expect perhaps as much beta radiation as gamma radiation. At a distance of 1 m from the beampipe the dose-rates are down to a couple of hundreds of mSv/h but it still looks from Figure 5 that people working on the beampipe or the inner detector will receive a full-body dose of something like 0.5-1 mSv/h.

For the vacuum group no interventions are needed in the short access scenario but in the long access scenario, when the beampipe has to be removed, there will of course have to be technicians working with the beampipe in this radiation environment. As long as the removal can be done quickly enough the radiation should not prevent the vacuum group from doing its job.

It will be more difficult for the inner detector group to do maintenance on the inner detector for prolonged periods of time. It is now being discussed within the inner detector community if maintenance should be foreseen with the VA beampipe in place or if all inner detector maintenance can be limited to the long access scenario. If this is not the case one have to consider some way of reducing the radiation from the beampipe. To install temporary shielding will be very difficult. One possibility would be to make the beryllium part of the beampipe longer but that is very costly. Another less expensive possibility would be to make the beampipe of aluminium. As can be seen in Figure 5 this would reduce the radiation with a factor of 11 after ten years of running (and even more for shorter running periods). A complication with this solution is the pump made of stainless steel that is situated just in front of the inner detector. If this pump cannot be made of aluminium the reduction of the dose-rate by going to aluminium will be less impressive than a factor of 11.

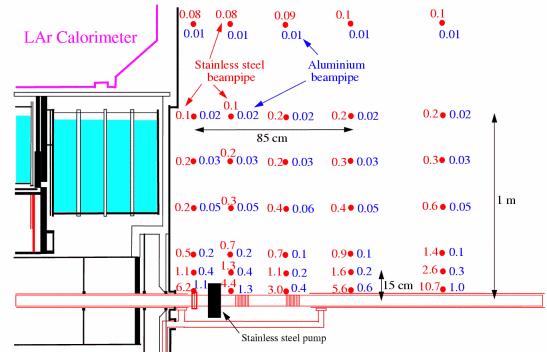
Figure 5: Predicted dose-rates in mSv/h from the VA beam pipe after 10 years of running and 5 days of cooling. The values for the aluminium beam pipe is for 1.5 mm thick tubes compared to 0.8 mm for the stainless steel case.

6 CONCLUSIONS

The predicted dose-rates from beampipes made of stainless steel, aluminium and beryllium have been presented. There are large differences between the radiation levels from the different materials. With a beryllium beampipe the dose-rates are a couple of mSv/h. For an aluminium beampipe the expected full-body dose-rate is a few hundreds of mSv/h after 10 years of running and a stainless steel beampipe will give a full-body dose-rate of 0.5-1 mSv/h already after one year of running. The dose-rates to the hands of a technician who removes a stainless steel beampipe can reach 10-15 mSv/h.

The above-mentioned dose-rates are uninteresting if they are not related to the work assumed to be done in this environment. The short and long access scenarios have therefore been discussed in some detail. The short access scenario should not be a problem for the vacuum group as long as beampipe supports are easily accessible. The long access scenario is more problematic and an assessment of the time needed to remove the beampipe will have to be made before one can say what implications the predicted radiation levels have.

For the maintenance of the inner detector the big question is if maintenance during the short access can be excluded. If that is not the case one can envision changing the material in the beampipe to beryllium or aluminium but this will result in a significant increase in cost and complexity.

7 REFERENCES

[1] The ATLAS activation studies http://atlasinfo.cern.ch/Atlas/TCOORD/Activities/CommonSys/Shielding/Activation/activation.html

[2] G.R. Stevenson, Activation at accelerators, CERN/TIS-RP/90-10/CF

[3] M. Hoefert and A. Bonifas, Measurement of radiation parameters for the prediction of dose rates from induced radioactivity, CERN Internal report HP-75-148 (1975)

[4] by M. Shupe at the Univ. of Arizona.

[5] C. Zeitnitz, The GCALOR simulation package

http://www.physik.uni-mainz.de/zeitnitz/gcalor/gcalor.html

[6] R. Engel and J. Ranft, Hadronic photon-photon interactions at high-energies,

Phys. Rev. D54(1996)4244

[7] V.A. Klimanov, E.I. Kulakova, M.N. Morev and V.K. Sakharov, Activation study of the ATLAS detector, ISTC Project #1800, April-June 2001, Moscow Engineering Physics Institute.

http://atlasinfo.cern.ch/Atlas/TCOORD/Activities/CommonSys/Shielding/Activation/report_1_2_new.pdf

[8] V.A. Klimanov, E.I. Kulakova, M.N. Morev and V.K. Sakharov, Activation dose rate in access scenarios to the area between the disk shield and the toroid, ISTC Project #1800, July-September 2001, Moscow Engineering Physics Institute.

http://atlasinfo.cern.ch/Atlas/TCOORD/Activities/CommonSys/Shielding/Activation/text_tab_1_4.pdf

[9] V.G. Semenov and N.M. Sobolevsky, Approximation of Radionuclide Production Cross section in Proton Induced Nuclear Reactions. Report on the ISTC project #187, Moscow, 1998

[10] F. Mynat et al., The DOT-III Two-Dimensional Discrete Ordinates Transport Code, ORNL-TM-4280, Oak Ridge, 1973.

[11] J.F. Briesmeister, MCNP - A general Monte Carlo N-Particle Transport Code, Version 4A, Los Alamos National Laboratory Report, LA-12625, 1995.

[12] M. Barbier, Induced Radioactivity, North Holland, Amsterdam, 1969.